First variation of area formula
In Riemannian geometry, the first variation of area formula relates the mean curvature of a hypersurface to the rate of change of its area as it evolves in the outward normal direction.
Let 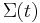 be a smooth family of oriented hypersurfaces in a Riemannian manifold M such that the velocity of each point is given by the outward unit normal at that point. The first variation of area formula is
be a smooth family of oriented hypersurfaces in a Riemannian manifold M such that the velocity of each point is given by the outward unit normal at that point. The first variation of area formula is
where dA is the area form on 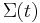 induced by the metric of M, and H is the mean curvature of
induced by the metric of M, and H is the mean curvature of 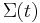 . The normal vector is parallel to
. The normal vector is parallel to  where
where  is the tangent vector. The mean curvature is parallel to the normal vector.
is the tangent vector. The mean curvature is parallel to the normal vector.
References
- Chow, Lu, and Ni, "Hamilton's Ricci Flow." AMS Science Press, GSM volume 77, 2006.
